实际工作中要处理的变量之间的关系往往是错综复杂的。处理这些多变量数据的最大挑战之一就是信息过度复杂,若数据集有100个变量,如何了解其中所有的交互关系呢?即使只有20个变量,当试图理解各个变量与其他变量的关系时,也需要考虑190对相互关系。主成分分析等方法是用来探索和简化多变量复杂关系的常用方法。在这里我们重点介绍两种简化多变量复杂关系,即降维的方法:主成分分析和t-SNE(t-Distributed Stochastic Neighbor Embedding)。(测试数据和代码见文末客服二维码)
PCA
主成分分析(Principle component analysis, PCA)前面我们已经用两期教程跟大家讲过理论和实际绘图(在线主成分分析Clustvis和主成分分析绘图)。今天,我们就从PCA的数理统计层面入手,去讲讲完整的PCA应该怎么操作。
总体而言,PCA是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关变量就称为主成分。例如,使用PCA可将30个相关(很可能冗余)的环境变量转化为5个无关的成分变量,并且尽可能地保留原始数据集的信息。主成分是观测变量的线性组合。形成线性组合的权重都是通过最大化各主成分所解释的方差来获得,同时还要保证各主成分间不相关。(本文中介绍的两种方法都需要大样本来支撑稳定的结果,但是多大样本量才足够也是一个复杂 的问题。目前,数据分析师常使用经验法则:“因子分析需要5~10倍于变量数的样本数。”)
R的基础安装包提供了PCA的函数,即函数princomp(),前面我们也曾经讲过。这里我们将重点介绍psych包中提供的函数。它们提供了比基础函数更丰富和有用的选项。主成分分析往往要经过一些常见的步骤,如:数据预处理、选择模型、判断要选择的主成分数目、选择主成分、旋转主成分、解释结果、计算主成分得分。下面的例子将会详细解释每一个步骤。
示例数据集USJudgeRatings包含了律师对美国高等法院法官的评分。数据框包含43个观测,12 个变量。由于示例数据本身规范无缺失值,所以直接选择主成分分析作为分析模型,下面是判断需要多少个主成分。判断主成分数目的准则一般有:
1,根据先验经验和理论知识判断主成分数;
2,根据要解释变量方差的积累值的阈值来判断需要的主成分数;
3,通过检查变量间k×k的相关系数矩阵来判断保留的主成分数。
利用函数fa.parallel(),你可以同时对三种特征值判别准则进行评价。该函数绘制的图片如图1。图中虚线表明选择一个主成分即可保留数据集的大部分信息。
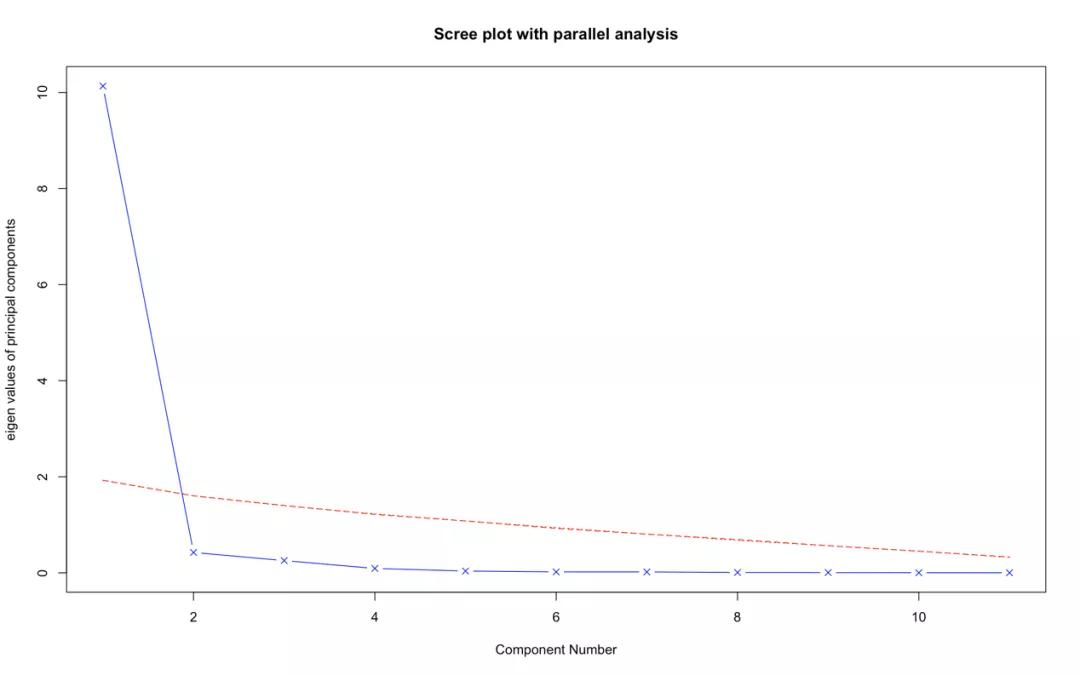 图1,判断主成分数目
图1,判断主成分数目
下一步是使用函数principal()挑选出相应的主成分。函数principal()可以根据原始数据矩阵或者相关系数矩阵做主成分分析。格式为:
1principal(r, nfactors=, rotate=, scores=)
其中:参数r是相关系数矩阵或原始数据矩阵;参数nfactors设定主成分数(默认为1);参数rotate指定旋转的方法(默认最大方差旋转);scores设定是否需要计算主成分得分(默认不需要)。示例数据的分析结果(1个主成分)如图2。
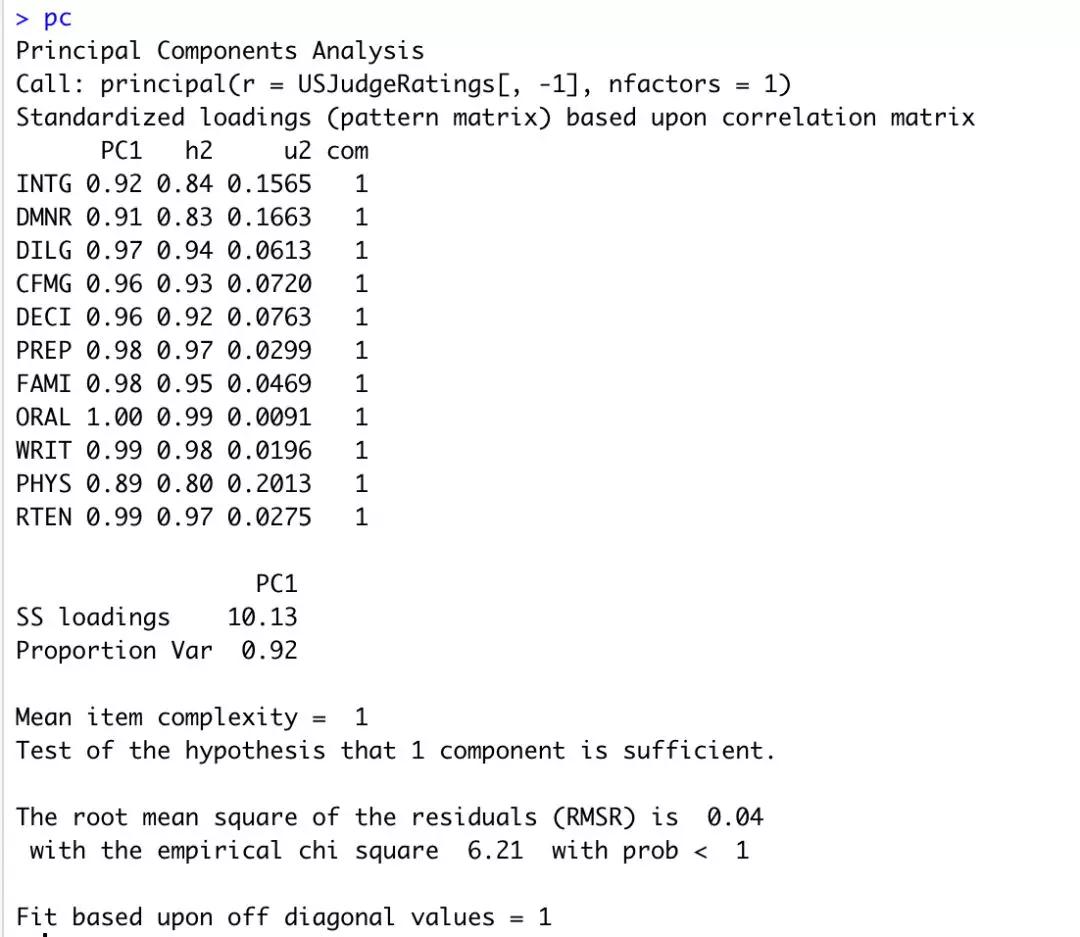 图2,提取主成分结果
图2,提取主成分结果
图中,PC1栏包含了成分载荷,指观测变量与主成分的相关系数。如果提取不止一个主成分,那么 还将会有PC2、PC3等栏。成分载荷(component loadings)可用来解释主成分的含义。此处可以看到,第一主成分(PC1)与每个变量都高度相关,也就是说,它是一个可用来进行一般性评价的维度。h2栏指成分公因子方差,即主成分对每个变量的方差解释度。u2栏指成分唯一性,即方差无法被主成分解释的比例(1–h2)。SS loadings行包含了与主成分相关联的特征值,指的是与特定主成分相关联的标准化后的方差值(本例中,第一主成分的值为10)。最后,Proportion Var行表示的是每个主成分对整个数据集的解释程度。此处可以看到,第一主成分解释了11个变量92%的方差。
下面在看一个主成分数目不为1的例子,Harman23.cor数据集包含305个女孩的8个身体测量指标。本例中,数据集由变量的相关系数组成,而不是原始数据集(如图3)。
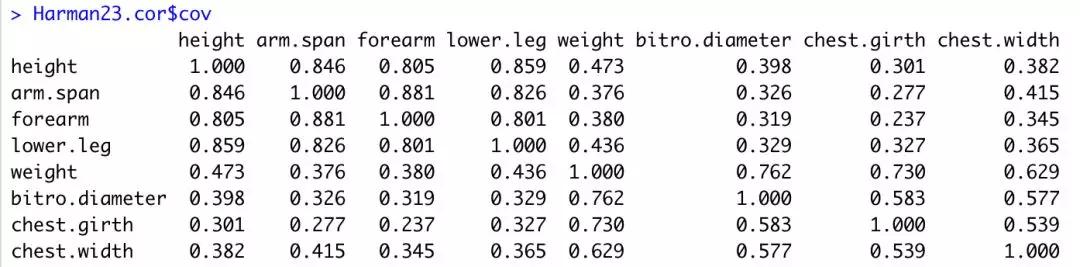 图3,Harman23.cor数据集
图3,Harman23.cor数据集
图4说明这次需要选择两个主成分。
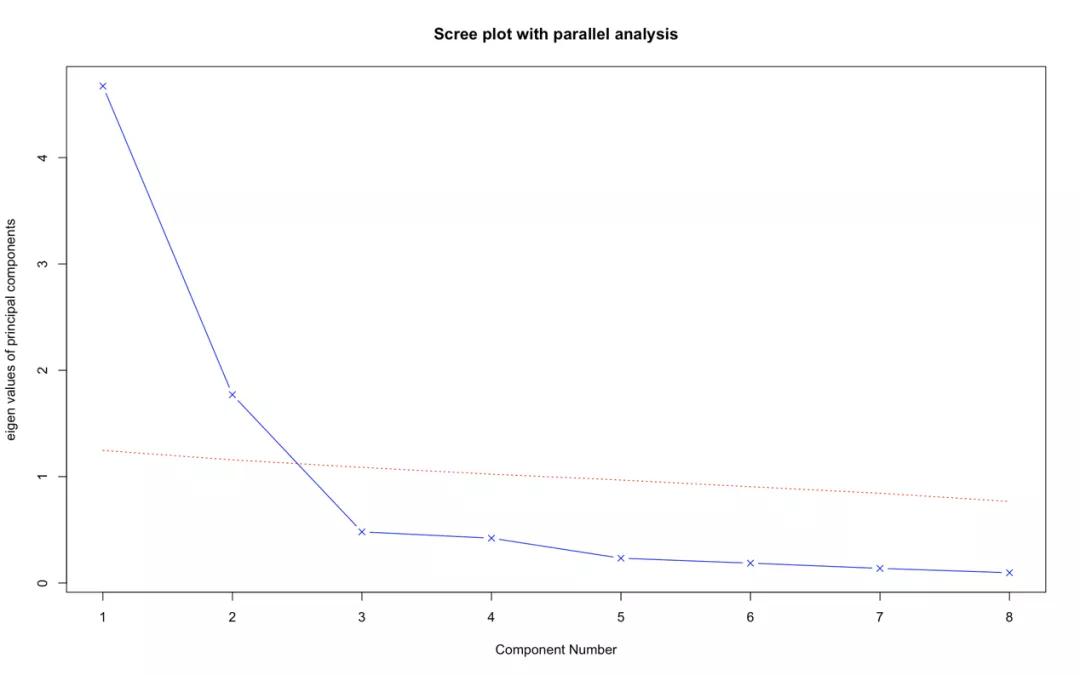 图4,Harman23.cor的主成分数目分析
图4,Harman23.cor的主成分数目分析
图5展示了两个主成分的提取结果。
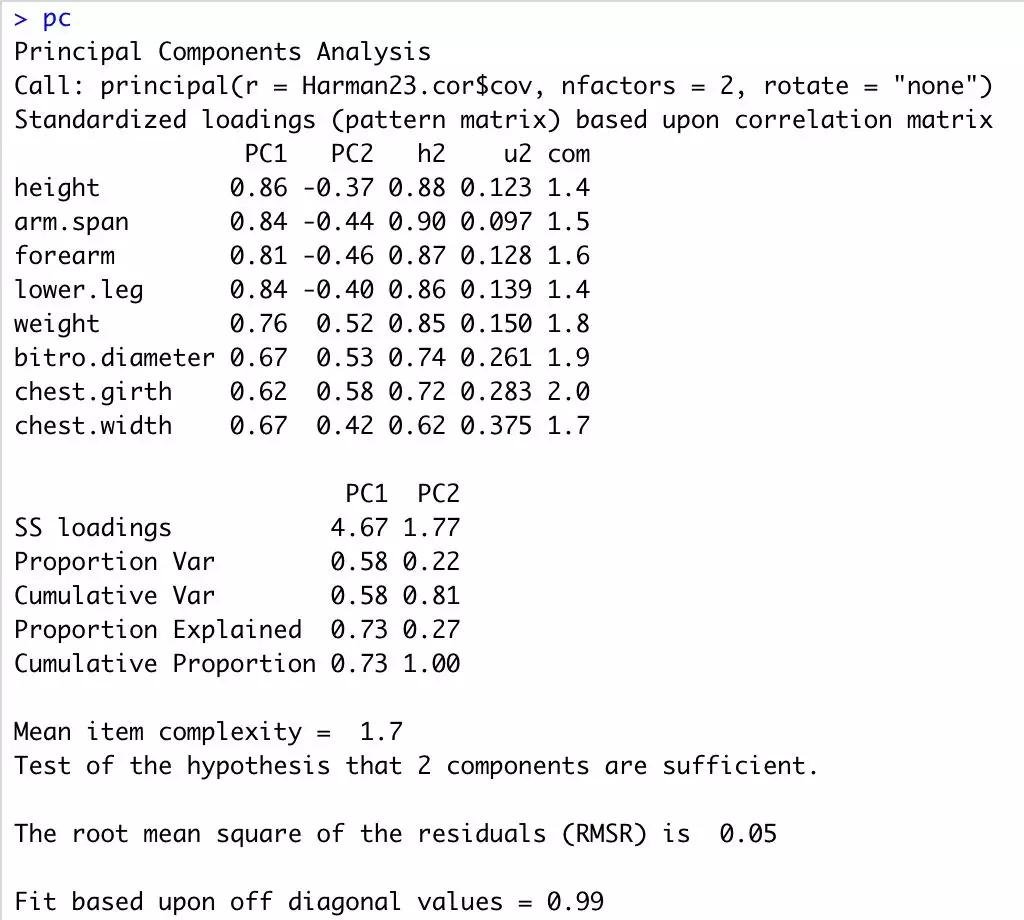 图5,Harman23.cor的主成分提取
图5,Harman23.cor的主成分提取
现在的问题是这些主成分的内在含义是什么呢?我们可以通过主成分旋转将成分载荷阵变得更容易解释,旋转方法有两种:使选择的成分保持不相关(正交旋转),和让它们变得相关(斜交旋转)。最流行的正交旋转是方差极大旋转,它试图对载荷阵的列进行去噪,使得每个成分只由一组有限的变量来解释(即载荷阵每列只有少数几个很大的载荷,其他都是很小的载荷)。现在对Harman23.cor使用方差极大旋转(结果如图6)。
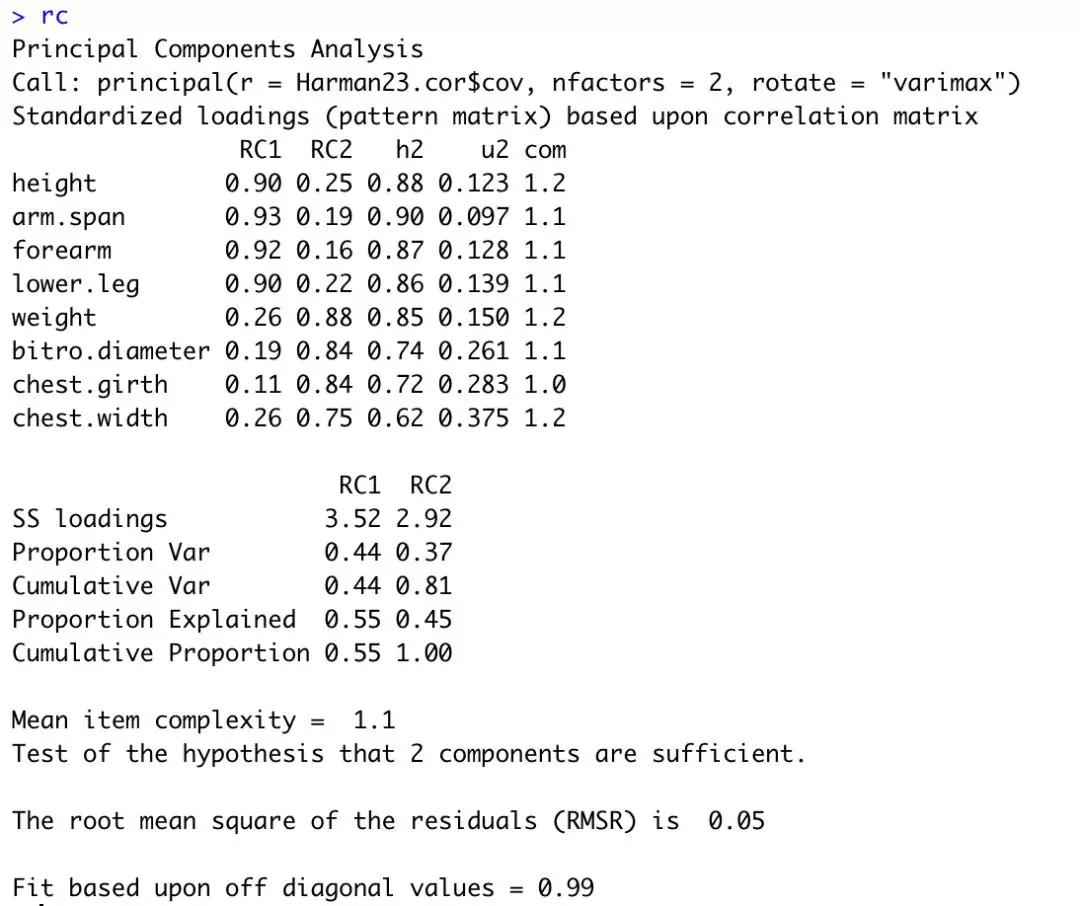 图6,主成分旋转的结果
图6,主成分旋转的结果
列的名字都从PC变成了RC,以表示成分被旋转。观察RC1栏的载荷,你可以发现第一主成分主要由前四个变量来解释(长度变量)。RC2栏的载荷表示第二主成分主要由变量5到变量8来解 释(容量变量)。但是我们的最终目标是用一组较少的变量替换一组较多的相关变量,因此,你还需要获取每个观测在成分上的得分。
回到第一个例子,我们根据原始数据中的11个评分变量提取了一个主成分。利用函数principal(),你很容易获得每个调查对象在该主成分上的得分,利用相关系数矩阵得到的主成分分析结果的主成分得分计算方法有所不同,但也比较简单(欲寻代码,见文末客服二维码)。
tSNE
到这里,主成分分析的部分就基本结束,显然主成分分析是一种线性相关的分析方法,而下面要介绍的t-SNE则适用于非线性关系,它的主要用处为降维,一般将高维数据转化为二维数据并绘制图形,便于我们观察变量之间的关系。目前t-SNE主要应用在图像处理(医学图像处理等)、文本比对等领域,在生物信息学也有很广阔的应用前景。在R语言中,包Rtsne整合了t-SNE算法。下面是两个简单的例子。第一个例子涉及到了数据集irisi。数据集中的五个变量如图7。
 图7,数据集irisi中五个变量
图7,数据集irisi中五个变量
下面我们利用函数Rtsne()将除了species之外的四个变量降为两个维度,并利用颜色标示变量species,绘制出降维后的数据。
 图8,数据集irisi降维结果
图8,数据集irisi降维结果
图中可以看到降维之后的三个物种比较理想的聚合在一起,但是也有部分离群的数据点。(如果你运行了后台的代码,你会发现你的图形并不是和图8完全一样,这是t-SNE的特点决定的,不必惊慌。)
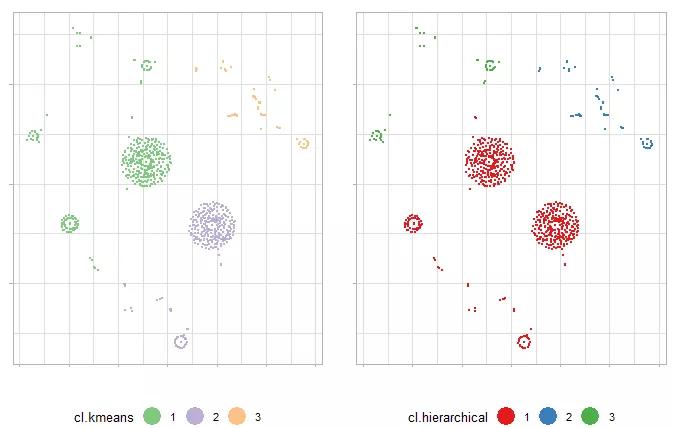
如果数据集本身没有给出数据点的分类,t-SNE的降维结果也可以用于分类,在后台我们提供data.txt作为示例数据,利用函数Rtsne处理之后,绘制对应的图像结果如图9。
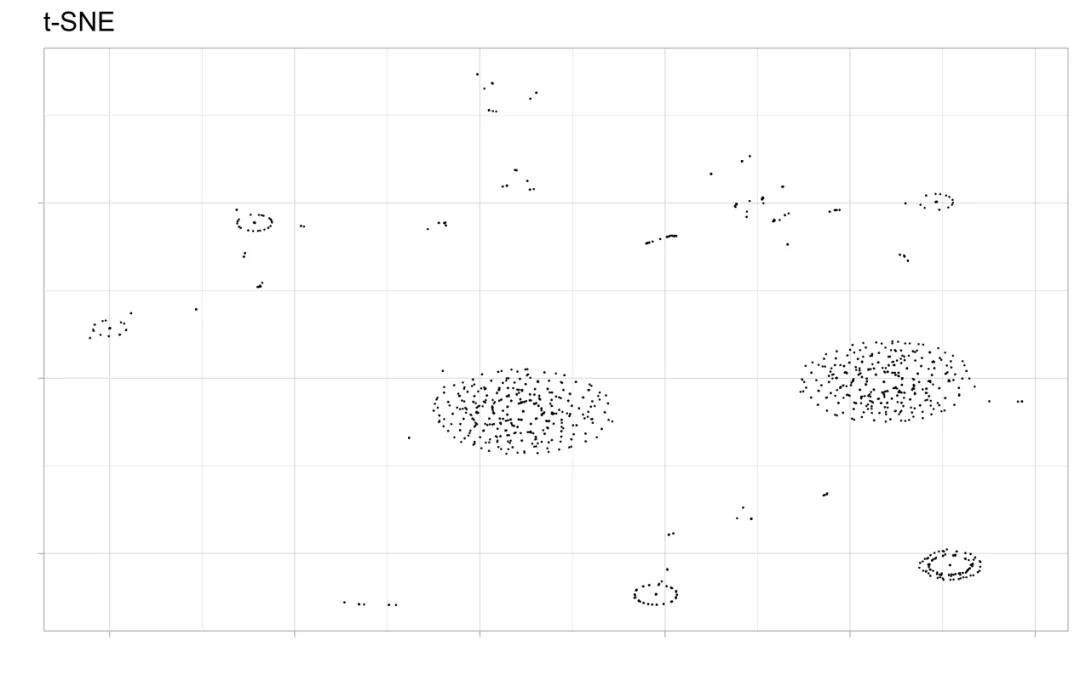 图9. 测试数据的处理结果
图9. 测试数据的处理结果
同样的,你的图形可能不太一样。同时,你也会发现,t-SNE算法在数据量增大之后的计算时间显著增加(t-SNE算法的复杂度也是一个不容忽视的问题)。
在后台代码中,我们提供了利用data.txt降维后的数据进行聚类并绘图的代码,在下次教程,我们会详细讲解有关的聚类方法,大家可以先自己熟悉起来。
本期干货
·
- PCA及tSNE代码 -
关注“科研猫”公众号,
- 本文固定链接: https://maimengkong.com/image/1148.html
- 转载请注明: : 萌小白 2022年8月19日 于 卖萌控的博客 发表
- 百度已收录
