【科研加油站】SPSS操作之两因素重复测量的方差分析

以下内容转载自“医咖会”微信公众号（medieco-ykh），作者李延龙。

上一期我们讨论了单因素重复测量方差分析，本期 “科研加油站”栏目，我们一起来探讨两因素重复测量的方差分析。

问题与数据

某研究者拟评估海水淹溺后残留于肺内的海水是否可导致严重的肺损伤，建立动物模型。将12只杂种犬随机分为两组，一组海水灌注右肺，另一组海水灌注全肺，每组6只。每只犬分别于海水灌注前以及灌注后5min、30min、60min、120min检测氧分压PaO2(kPa)。（案例来自于刘桂芬《医学统计学》）

试问：

（1）不同灌注处理对肺部氧分压有何作用？

（2）时间是否也会产生影响？

（3）两者之间是否存在交互作用？

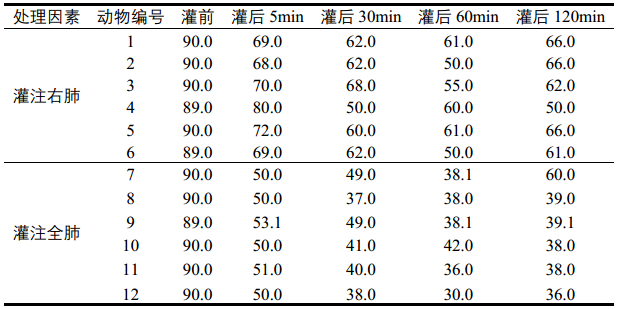
表1　海水灌注前后两组杂种犬的PaO2(kPa)测定结果

对数据结构的分析

整个数据资料涉及两组研究对象，旨在比较两组灌注部位氧分压有无差别。与我们以往所知道的完全随机设计或者随机区组设计（研究对象被随机分配到各处理组，观察各组结局指标一次测量结果）不同，本研究对结局指标（氧分压）进行了多次测量；另外，每个观察对象在灌注前以及灌注后5min、30min、60min、120min检测的氧分压PaO2(kPa) 是相关的。这就是我们常见的重复测量设计。

由于重复测量时，每个个体的测量结果之间存在一定程度的相关，违背了方差分析数据独立性的要求，如果仍使用一般的方差分析，将会增加犯I类错误的概率，所以重复测量资料有相对应的方差分析方法。

重复测量方差分析要求各时点指标变量满足球形假设(Sphericity 假设)，通常用Mauchly方法检验是否满足球形假设，若检验结果P>0.05，认为满足；若P<0.05，则不满足。当资料满足球形假设时，可直接进行一元方差分析；不满足时，应以多元方差分析结果为准（图1）。

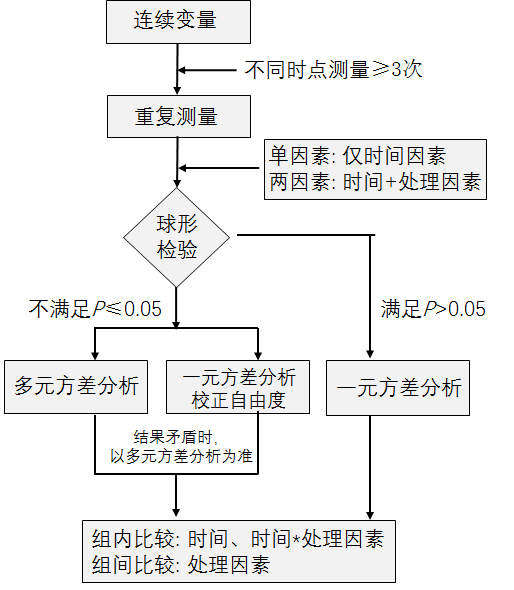
图1　两因素重复测量方差分析

SPSS分析方法

1. 数据录入

(1) 变量视图

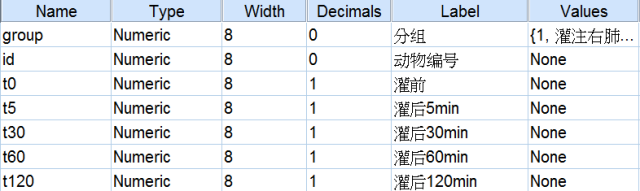
(2) 数据视图

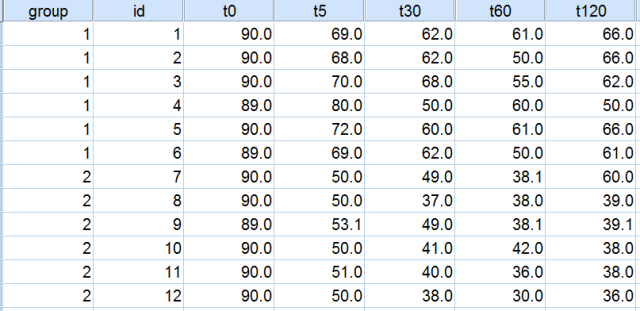
2. 选择Analyze→General Linear Model→Repeated Measures

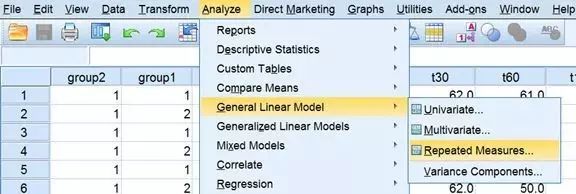
3. 选项设置

(1) Within-Subject Factor Name框中输入“time”，Number of Levels框输入“5”（这里因为每个研究对象重复测量了5次）→Add→Define

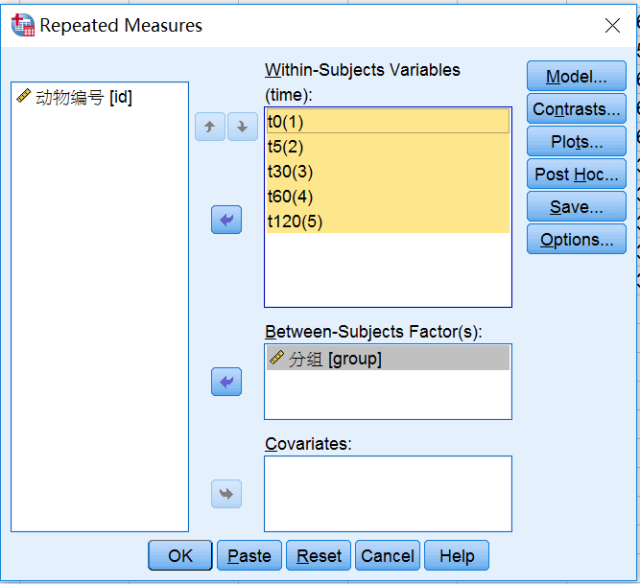
(2) 主对话框设置：将各时间点观测变量t0-t120放入Within-Subjects Variables(Time)框中→将分组变量group放入Between-Subjects Factor(s)框中。

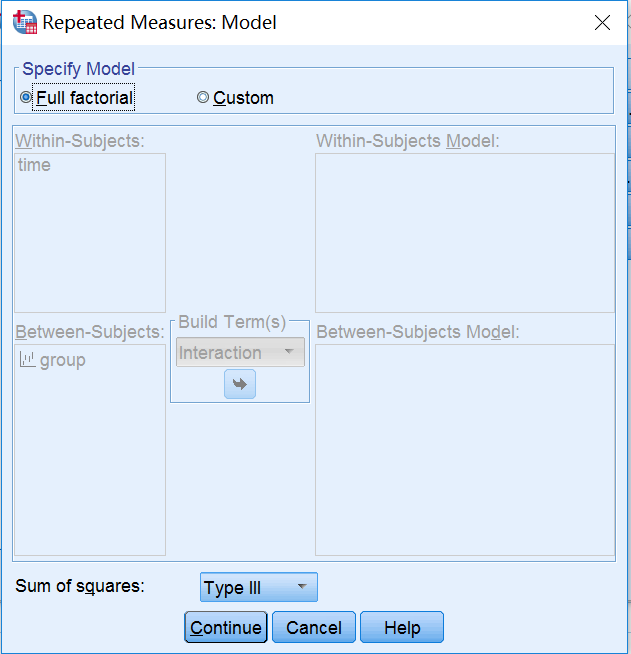
(3) Model设置：Specify Model默认Full factorial，输出处理因素和时间的主效应，以及两者的交互效应检验的结果。Sum of squares选择Type Ⅲ，这里适用于平衡数据，即各组样本例数相同。对于非平衡数据，选择Type Ⅳ → Continue。

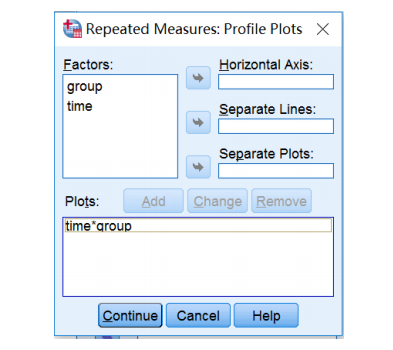
(4) Plots设置：将time放入Horizontal Axis框，group放入Separate Lines框→ Add → Continue，这里定义横坐标为time，分组为group，绘制time与group的轮廓图。

(5) Post Hoc设置：如果group≥3组，可将group放入Post Hoc Tests for框中，勾选恰当的检验方法，进行两两比较。本案例中仅有两组，不需要设置→Continue

(6) Options设置：勾选Deive statistics，用于不同处理组各个时点指标变量的统计描述→Continue→OK

结果解读

表2　统计描述

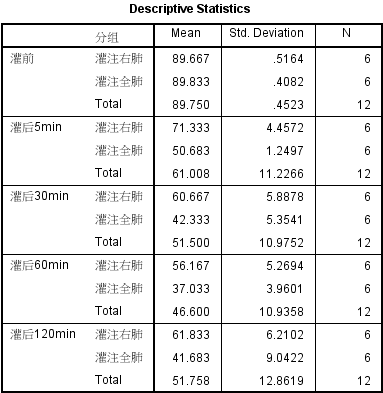
表3　球形检验结果

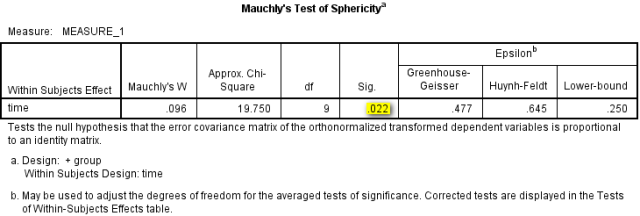
表4　组内因素的多元方差分析检验结果

表5　组内因素的一元方差分析检验结果

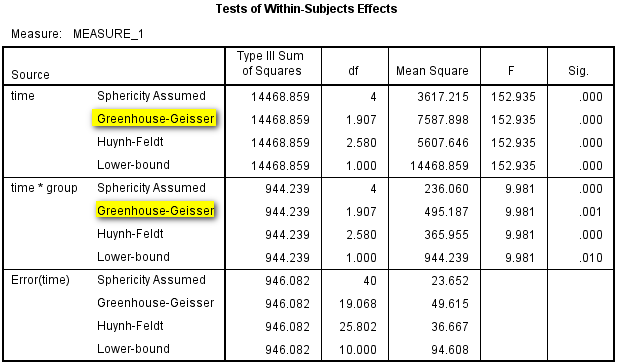
表6　组间因素的一元方差分析检验结果

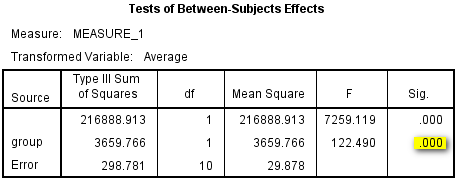
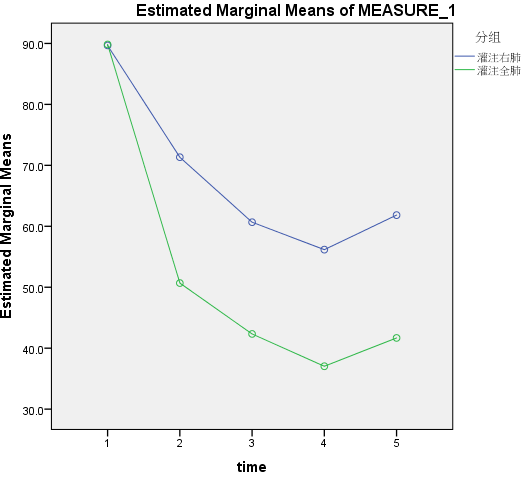
图2　时间与处理因素轮廓图

（1）组内比较：本案例中球形检验结果P=0.022<0.05，数据不满足球形假设，应以多元方差分析结果为准，即表4第1行和第5行（SPSS会给出4种检验方法，一般以Pillai's Trace结果为准），同时也可以参考校正后的一元方差分析结果，多推荐Greenhouse-Geisser的校正结果，即表5第2行和第6行。这里time和time*group均有P<0.05，提示各个时点指标变量存在差异，且处理因素对于指标变量的作用会随着时间的变化而变化（可参考图2）。

如果这里数据满足球形假设，可直接进行一元方差分析，无需校正，应采用表5第1行和第5行结果。

（2）组间比较：表6给出处理因素group的方差分析，P<0.001，提示不同灌注部分之间氧分压存在差异。

撰写结论

不同灌注部位处理的肺部氧分压差别有统计学意义，全肺灌注的氧分压低于单肺灌注的氧分压；灌注海水的时间也有影响，海水灌注后，犬的氧分压逐渐下降，到灌注后60min达到最低，之后有小幅上升；灌注部位和时间之间存在交互效应，随灌注时间的延长，单肺灌注与全肺灌注氧分压下降幅度不同，以全肺灌注组的下降幅度最大。

备注

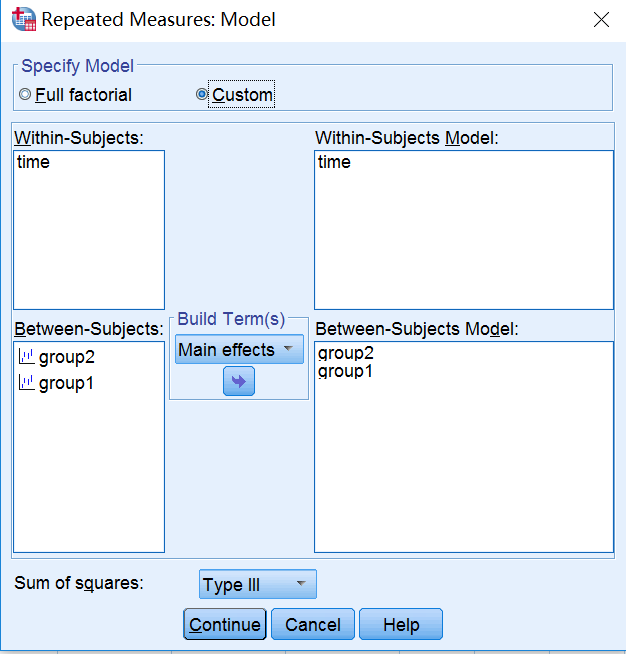
多因素重复测量的方差分析往往存在多个处理因素，这时候需要单独考虑多个处理因素之间的交互作用，若一个研究有两个处理因素，即group1和group2，这时SPSS中Model设置先使用默认的Full factorial，会考虑group1*group2交互是否存在，如果交互检验不存在统计学意义，需要进一步使用Custom进行自定义，仅考虑group1和group2的主效应（如下图），并对结果进行相应的解读。