导读
一、SPSS 数据分析—描述性统计分析
二、spss 常见统计图形
一、SPSS 数据分析—描述性统计分析
SPSS 用于描述性统计分析的过程大部分都在分析—描述统计菜单中,另有一个在比较均值—均值菜单,虽然这几个过程用途不同,但是基本上都可以输出常用的指标结果。
1、分析—描述统计—频率
此过程可以输出连续型变量集中趋势和离散趋势的主要指标,还可以输出判断分布的直方图、峰度值和偏度值,此外,该过程最主要的作用是输出频数表。结果举例如下:
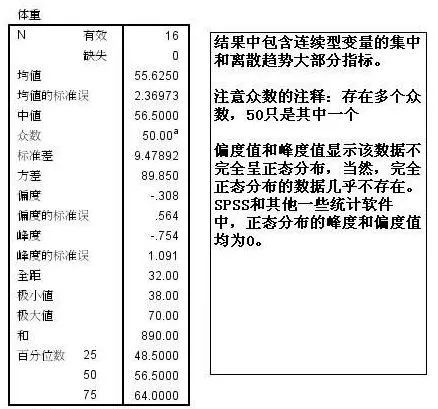
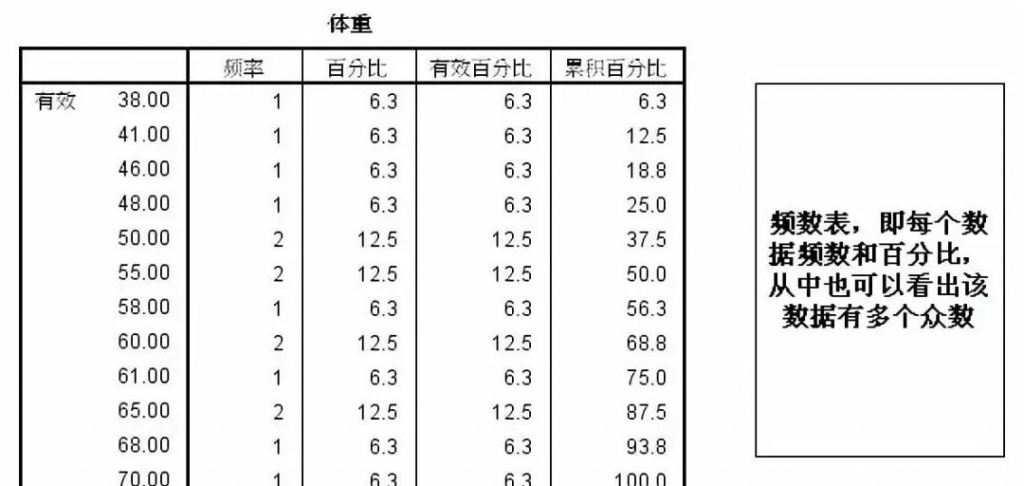
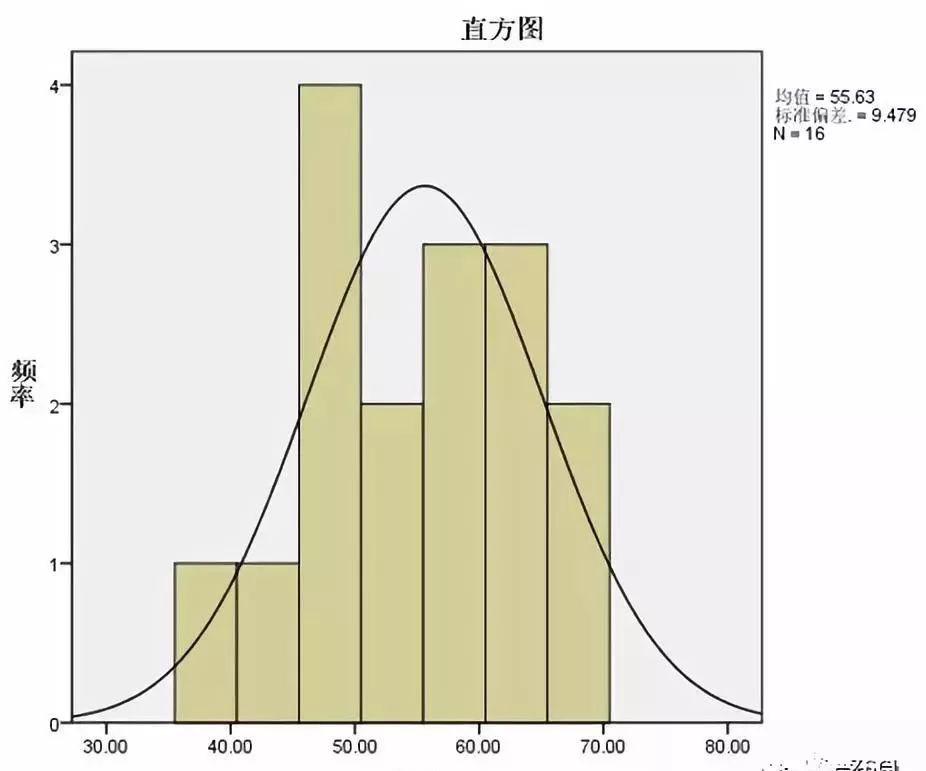
2、分析—描述统计—描述
看起来似乎这个过程才是正统的描述统计分析过程,实际上该过程输出的内容并不多,也没有统计图可以调用,唯一特别的是该过程可以对数据进行标准化变换,并保存为新变量。

3、分析—描述统计—探索
探索性分析是对原有数据进行描述性统计的基础上,更进一步的描述数据,和前两种过程相比,它能提供更详细的结果。


选择M-estimation复选项,求出集中趋势的稳健估计,该统计量是利用迭代方法计算出来,一般来说受异常值影响要小的多。如果该统计量离均数和中位数较远,则说明数据中可能存在异常值,此时宜用该估计值替代均数以反映集中趋势。一共会输出Huber、Andrew、Hampel和Tukey四种M统计量,其中Huber法适用于数据接近正态分布的情况,另三种则适用于数据中有许多异常值时;
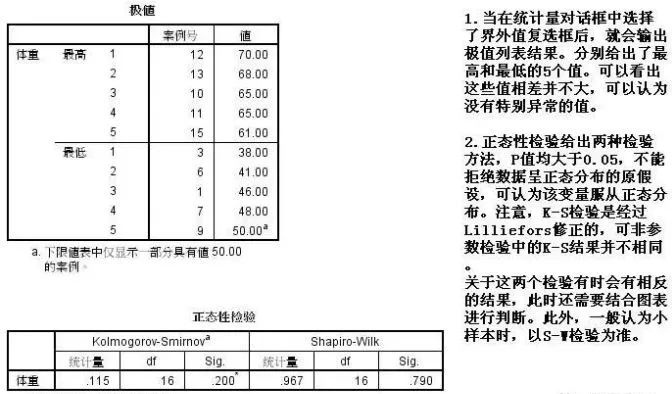
4、分析—描述统计—比率
该过程主要用于对两个连续变量间的比率进行描述分析。
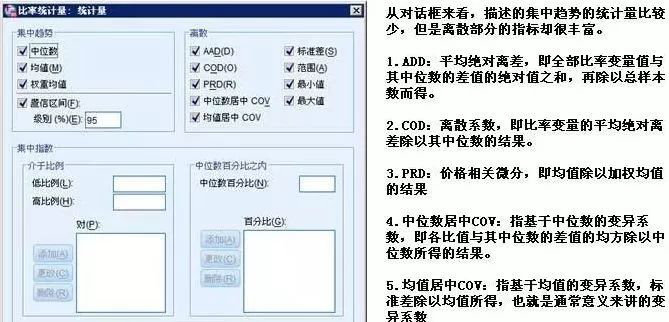
输出的结果比较简单,只是指标的汇总表格,在此略去
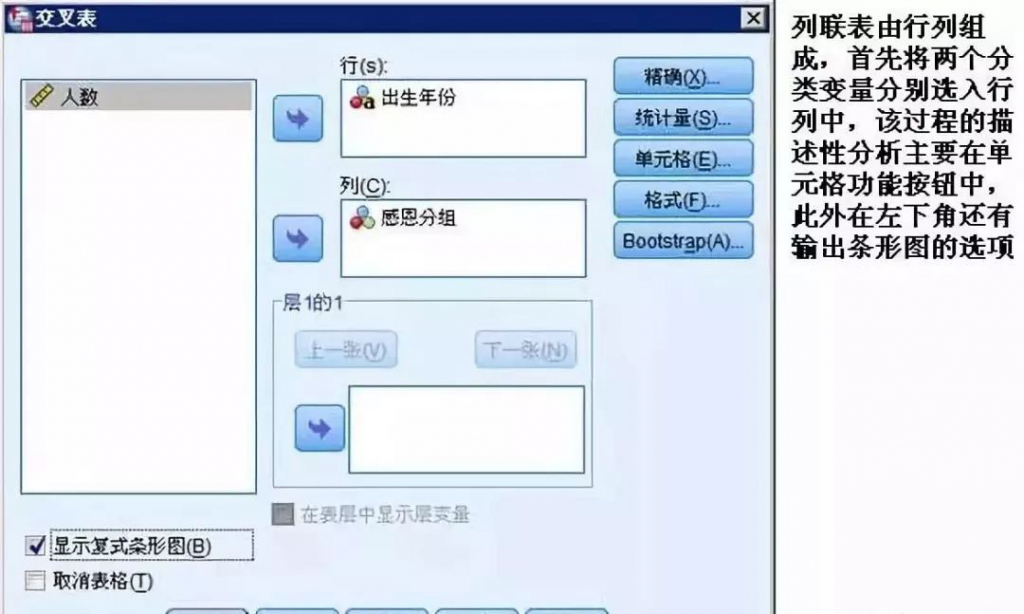
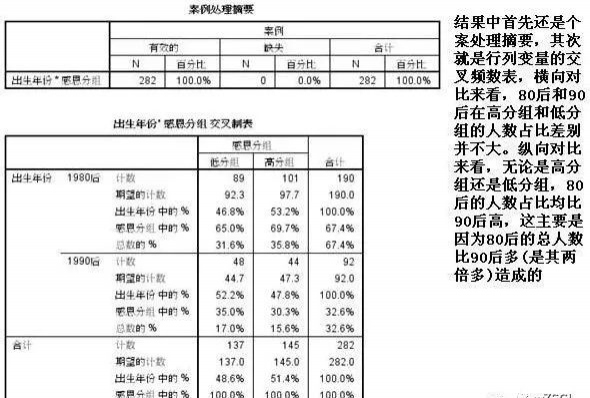
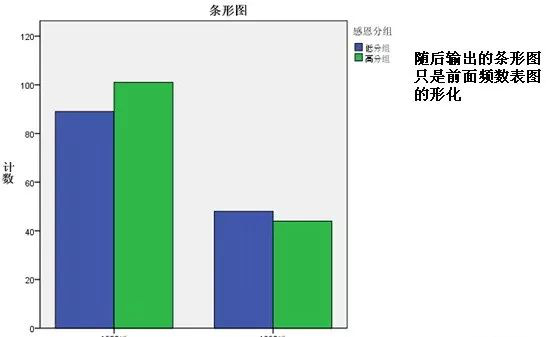
5、分析—描述统计—交叉表
分类变量的描述性统计比较简单,主要就是看频数分布和构成比,基本用交叉表一个过程就可以完成,该过程虽然放在描述统计中,但是由于功能丰富,也经常被用来做列联表的推断分析。
二、spss 常见统计图形
统计图能够简洁、直观地对主要的数据信息进行呈现,反映事物内在的规律和关联。当然难免会丢失数据的细节,鱼与熊掌不可兼得。
根据统计图呈现变量的数量将其分为单变量图、双变量图、多变量图,然后再根据测试尺度进行细分。变量主要分为 3 类:无序、有序和连续型变量。
1、单变量图:连续型变量
包括直方图、茎叶图、箱图、P-P 图等。
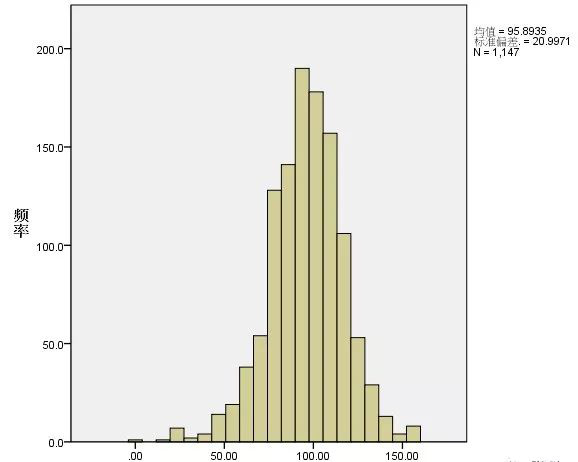


P-P图和Q-Q图主要用来判断正态分布。P-P图和Q-Q图的目的性基本一致,但原理上有着区别。
-
P-P图,其原理在于如果数据正态,那么数据的累积比例与正态分布累积比例基本保持一致。分别计算出数据累积比例,和假定正态时的数据分布累积比例;并且将实际数据累积比例作为X轴,将对应正态分布累积比例作为Y轴,作散点图。
请点击输入图片描述
p-p图
-
Q-Q图,其原理在于如果数据正态,那么其假定的正态分位数会与实际数据基本一致。计算出假定正态时的数据分位数;并且将实际数据作为X轴,将假定正态时的数据分位数作为Y轴,作散点图。

请点击输入图片描述
无论是P-P图,或者Q-Q图;如果说数据呈现出正态性,那么散点图看上去应该近似呈现为一条对角直线,此时说明数据呈现出正态性。如果散点图看上去明显不是一条直线,那么说明数据很可能不具有正态特质。P-P图和Q-Q图均可使用SPSSAU在线分析软件生成,两者功能一致看使用偏好选择即可。

2、单变量图:分类变量
包括饼图、简单条图、Pareto 图。
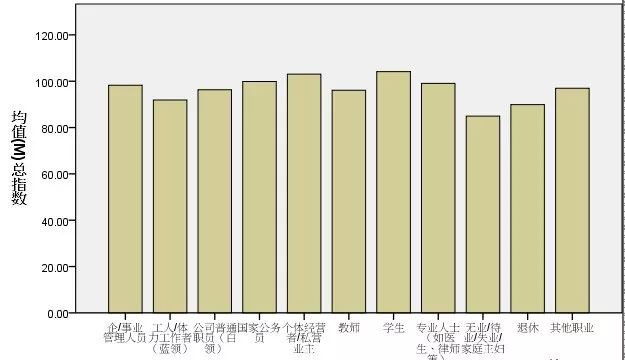
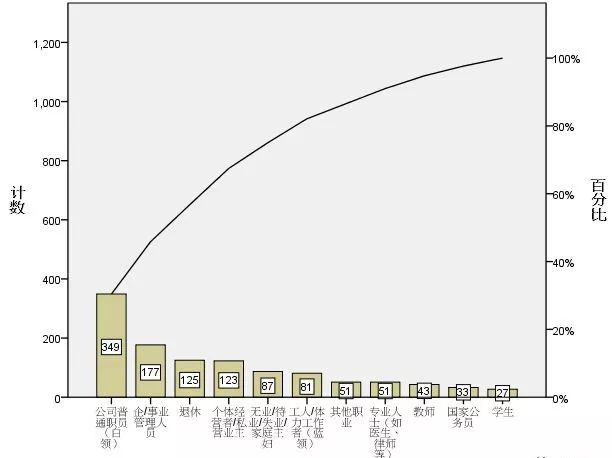
3、双变量图:连续应变量
即应变量为连续性变量的情形。注意此处 " 应 " 字并非笔误,应变量可理解为数学方程中的因变量。
此时又可分为三种情况,当另一个主动变化的变量(自变量)为:
(1)无序分类变量:简单条图。
(2)有序分类变量:线图,条图。用于直观表现随着有序变量的变化,应变量是如何上升或下降的。
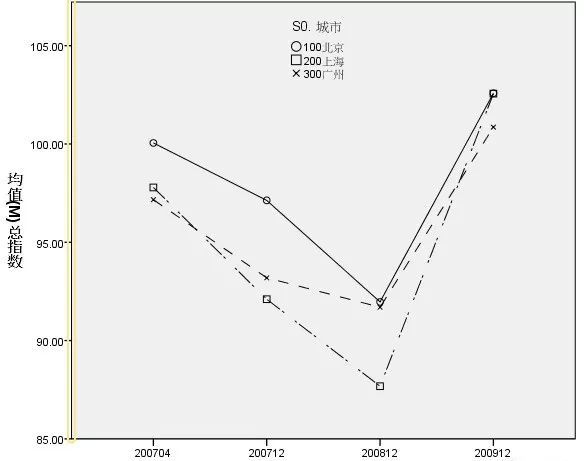
(3)连续性变量:散点图。用散点的疏密程度和变化趋势来对两个连续变量间的数量联系进行呈现。
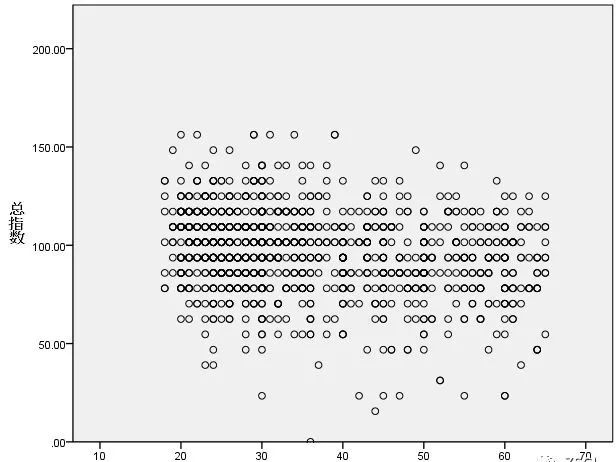
4、双变量图:分类应变量
当自变量为:
(1)分类变量:条图。按具体呈现方式,又可分为:复式条图、分段条图和马塞克图 3 种。
(2)连续变量:目前没有很好的图形可用。常见处理方式是,将自 / 应变量交换后用条图呈现。
以上介绍的双变量图仅是正规和常见的,其实还可利用单变量图的特性,当自变量为分类变量时,可分类别绘制相应单变量图进行呈现,常见的有分组箱图、复式饼图、直方图组。

5、多变量图
此处仅介绍 3 变量图,切勿将统计图做得太复杂,不然将失去统计图 " 直观明了 " 的优点。
要表现 3 个变量的关联,最好是采用三维坐标的立体统计图,但由于实际上还是在平面上对三维图呈现,立体图在使用上并不方便。
(1)当其中有变量为分类变量时,可以对二维图进行扩充,使二维图能够表现更多信息。例如在散点图中用点的形状或者颜色区分不同类别,其实就是呈现了两个连续变量和一个分类变量的数量关联信息。类似的还有多线图。
(2)当所有变量均为连续变量时,则上面的方法就不可用了。需要高维的散点图才行,SPSS 提供了一系列功能,如散点图矩阵、立体散点图和动态旋转等。
6、其它特殊用途的统计图。
(1)满足某一行业特殊需求:如用于将统计数据与地域分布相结合的统计地图、用于工业质量控制的控制图、用于股票分析的高低图。
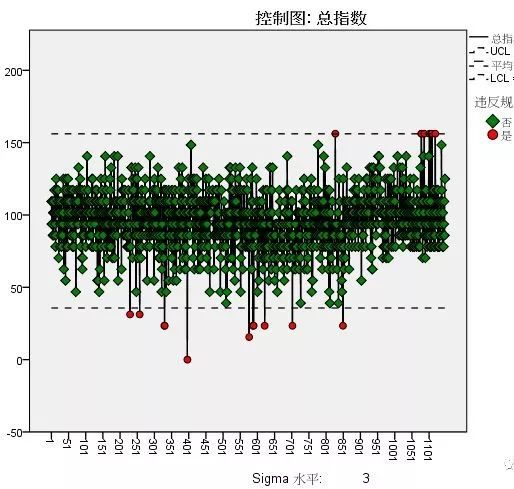
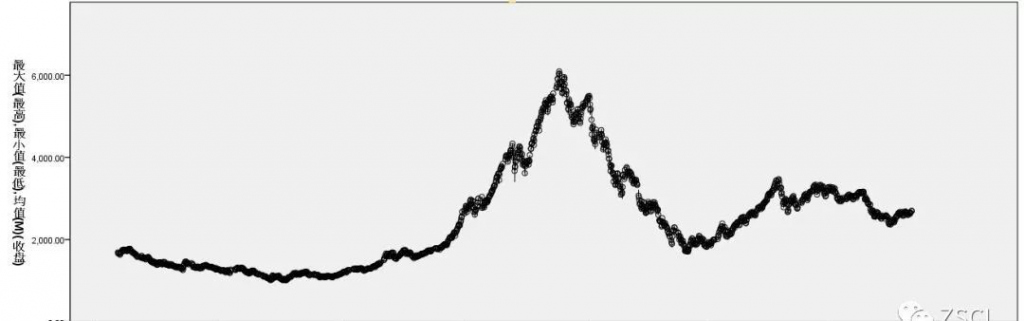
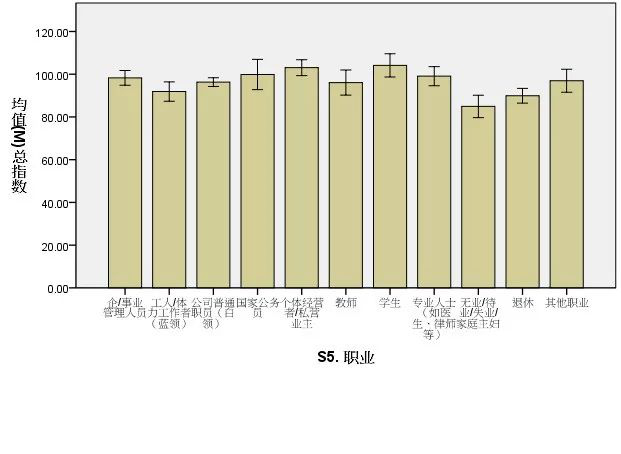
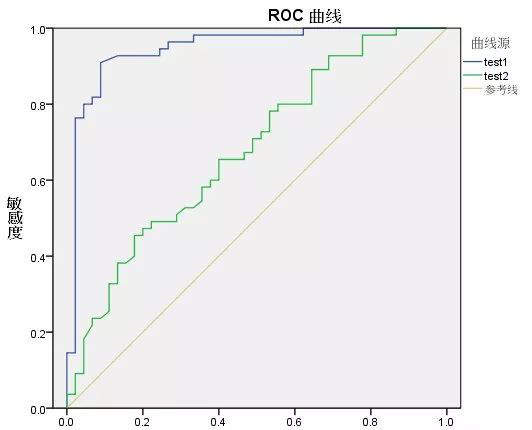
(2)解决某种专门的统计分析问题:用于描述样本指标可信区间或分布范围的误差条图、用于诊断性试验效果分析的 ROC 曲线、用于时间序列数据预分析的序列图。
▼
- 本文固定链接: https://maimengkong.com/kyjc/596.html
- 转载请注明: : 萌小白 2020年2月4日 于 卖萌控的博客 发表
- 百度已收录

