什么是生物统计学
生物统计学是一种很有用的工具,正确使用这一工具可以使科学研究更加有效,使科学研究可以更加高效的开展。因此,它是每位生物科学工作者必须掌握的基础知识。联川生物近日对生物统计学进行了系统式的学习,所用的教材——《生物统计学基础(原书第5版)》是一本非常有特色的书,与其他同类书比较,其有以下几类优点:
①教材内容通俗易懂但又非常严谨、细致、深入而又全面。书中的多数公式都有证明,且多用初等数学方法证明,对于不能用初等方法证明的也都给出了出处。
②本书核心是医学应用,作者通过大量的医学实例,引入及介绍统计方法,从如何构思到分析结果的解释,几乎都有全过程。由于一切从实用出发,所以对实用极为重要的知识,比如功效(power) 及样本量的估计,都是实际工作者极为关心的。
③学术上的先进性。作者将每个版本中的当时国际上最流行的统计方法及统计软件及时吸收在了本书内。
得“秘籍”如此,专业知识及科研水平定会有质升的提高!故此,小编为大家推出“生物统计学基础”相关知识系列课,和大家一起探索这本书里的珍贵知识,今日推送第六课:统计学-三大相关性系数!
统计学之三大相关性系数
一、统计学之三大相关性系数
三个相关性系数(pearson, spearman, kendall)反应的都是两个变量之间变化趋势的方向以及程度,其值范围为-1到+1,0表示两个变量不相关(相互独立),正值表示正相关,负值表示负相关,值越大表示相关性越强。
1. person correlation coefficient(皮尔森相关性系数)
公式如下:

其中的两个变量(X, Y)的皮尔森相关性系数(ρX,Y)等于它们之间的协方差cov(X,Y)除以它们各自标准差的乘积(σX, σY)。
以下对其进行详解:
① 公式的分母是变量的标准差,这就意味着计算皮尔森相关性系数时,变量的标准差不能为0(分母不能为0),也就是说你的两个变量中任何一个的值不能都是相同的。如果没有变化,用皮尔森相关系数是没办法算出这个变量与另一个变量之间是不是有相关性的。

计算得到皮尔森相关性系数的值为0.9481367,说明X1和Y1两个变量的相关性很高,并且还是正相关的关系。比如,实验中某种药物的给药剂量与实验对象的某个性状的变化,这两者关系很大,拿到这个统计学结论是不是很开心呢?
但是,如果X1变成了X2,X2内部的数据没有任何变化,那么计算X2与Y1的皮尔森相关性系数,会发生什么变化呢?
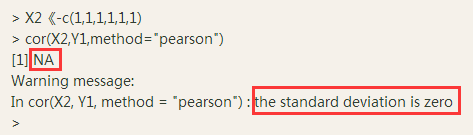
我们发现,计算的结果显示为NA,并且会提示标准差的结果是0,说明皮尔森相关性系数在这两个变量中是无法计算的。这就验证了前面提到的,两个变量中任何一个的值不能都是相同的,也就是说,X2的内部数值没有波动,那么它与Y2的相关性就不能通过皮尔森相关性系数来计算。
② 实验数据通常假设是成对的来自于正态分布的总体。
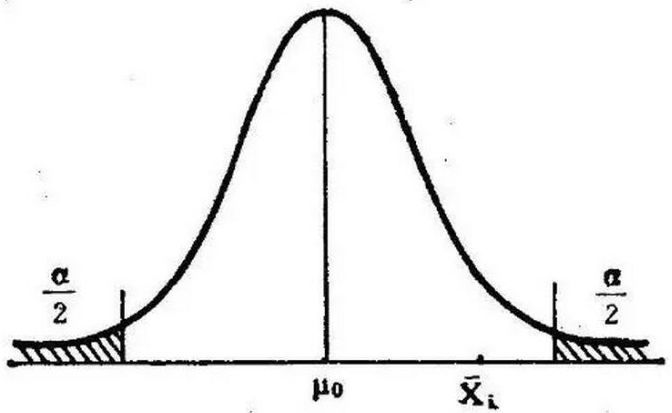
③ 实验数据之间的差距不能太大,或者说皮尔森相关性系数受异常值的影响比较大。因为公式的分母是变量各自标准差的乘积(σX, σY),所以说变量组内数据差异太大,对应标准差的乘积也会很大,因此皮尔森相关性系数的计算值相比较真实值,差异也会很大。
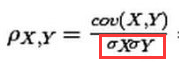
2. spearman correlation coefficient(斯皮尔曼相关性系数)
公式如下:
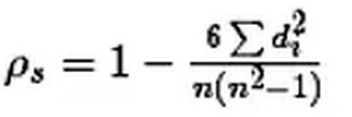
计算过程就是:首先对两个变量(X, Y)的数据进行排序,然后记下排序以后的位置(X’, Y'),(X’, Y')的值就称为秩次,秩次的差值就是上面公式中的di,n就是变量中数据的个数,最后带入公式就可求解结果。
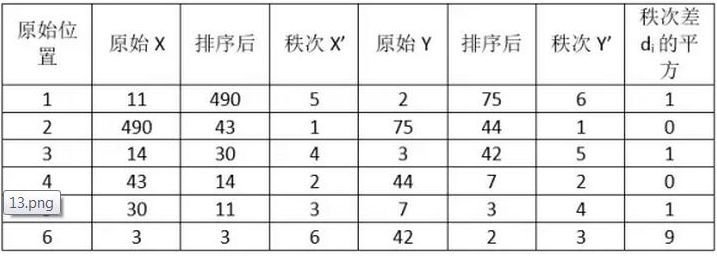
带入公式,求得斯皮尔曼相关性系数:
ρs= 1-6*(1+1+1+9)/6*35=0.657
当然也可以通过代码实现,如下所示:
> X《-c(11,490,14,43,30,3)
> Y《-c(2,75,3,44,7,42)
> cor(X,Y,method="spearman")
[1] 0.6571429
由以上计算,我们可得出以下结论:
① 不管X和Y这两个变量具体的值到底差了多少,只需要算一下它们每个值所处的排列位置的差值,就可以求出相关性系数了。
② 即便在变量值没有变化的情况下,也不会出现像皮尔森系数那样分母为0而无法计算的情况。另外,即使出现异常值,由于异常值的秩次通常不会有明显的变化(比如过大或者过小,那要么排第一,要么排最后),所以对斯皮尔曼相关性系数的影响也非常小。
③ 由于斯皮尔曼相关性系数没有那些数据条件要求,适用的范围就广多了。在我们生物实验数据分析中,尤其是在分析多组学交叉的数据中说明不同组学数据之间的相关性时,使用的频率很高。
3. kendall correlation coefficient(肯德尔相关性系数)
肯德尔相关性系数,又称肯德尔秩相关系数,它也是一种秩相关系数,不过它所计算的对象是分类变量。
分类变量可以理解成有类别的变量,可以分为:
无序的,比如性别(男、女)、血型(A、B、O、AB);
有序的,比如肥胖等级(重度肥胖,中度肥胖、轻度肥胖、不肥胖)。
通常需要求相关性系数的都是有序分类变量。
比如评委对选手的评分(优、中、差等),我们想看两个(或者多个)评委对几位选手的评价标准是否一致;学科老师在期末给某个学生的综合素质进行评价(优秀,中等,较差),我们想要知道各个学科老师对这位学生的评价是否一致;等等,这时候就可以使用肯德尔相关性系数进行衡量。
例如,用cor函数计算,把method这个参数设成“kendall”,这时我们假设评价等级---3表示优,2表示中,1表示差:
> X《-c(3,1,2,2,1,3)
> Y《-c(1,2,3,2,1,1)
> cor(X,Y,method="kendall")
[1] -0.2611165
根据以上计算,我们把X当成数学老师,把Y当成语文老师,那么从肯德尔相关性系数的计算的结果来看,这两位老师对该学生的评价是呈相反趋势的,不过这种相反的程度不很大。
生活中很多事物都可以用统计学的方法进行量化计算,是不是很神奇?
今天的生物统计学系列课就此结束~
- 本文固定链接: https://maimengkong.com/kyjc/1027.html
- 转载请注明: : 萌小白 2022年6月23日 于 卖萌控的博客 发表
- 百度已收录
