当你在做数据总结分析,或者科研调查分析,甚至季度年度总结汇报,需要查看数据的分布情况以及是否有异常情况来形成结论辅助进一步分析时,那么哪种图表能够清晰直观地展现出这一信息呢?
答案只有一个,那就是...箱线图!
什么是箱线图
箱线图,又名为盒须图,盒式图,通常用于展示一组数据的分布情况,因为主题形状像一个箱子,所以得名箱线图。它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比较。
箱线图是由美国著名的统计学家约翰.图基发明的,它主要展现了一组数据的几个关键数据点,包括最大值、最小值、中位数以及上下两个4分位数。也就是说,无论一组数据的量有多少,它只会在计算后,获取这几个计算后的数据来作为数据点,来绘制箱线图。
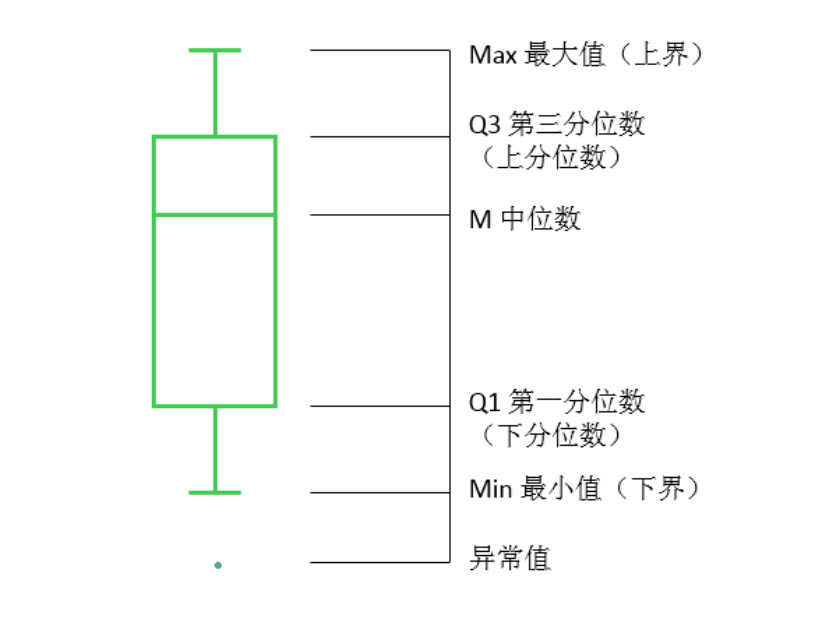
在箱线图中,箱子的中间有一条线,代表了数据的中位数。箱子的上下底,分别是数据的上四分位数(Q3)和下四分位数(Q1),这意味着箱体包含了50%的数据。因此,箱子的高度在一定程度上反映了数据的波动程度,上下边缘则代表了该组数据的最大值和最小值。有时候箱子外部会有一些点,可以理解为数据中的“异常值”。
我们先看一个简单的箱线图应用,大家就应该很好理解了。分析不同学年、不同科目的学生成绩是箱线图的常见应用场景,下图中我们可以看到学生的英语成绩相对其它科目普遍较好,而数学则大部分都在80分以下。
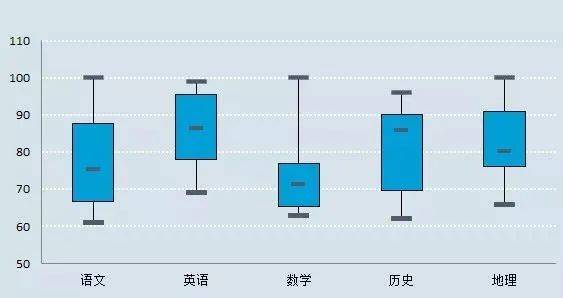
所以要快速理解箱线图,那么一定要了解这2个概念:
四分位数
一组数据按照从小到大顺序排列后,把该组数据四等分的数,称为四分位数。第一四分位数 (Q1)、第二四分位数
(Q2,也叫“中位数”)和第三四分位数
(Q3)分别等于该样本中所有数值由小到大排列后第25%、第50%和第75%的数字。第三四分位数与第一四分位数的差距又称四分位距(interquartile
range, IQR)。
偏态
与正态分布相对,指的是非对称分布的偏斜状态。在统计学上,众数和平均数之差可作为分配偏态的指标之一:如平均数大于众数,称为正偏态(或右偏态);相反,则称为负偏态(或左偏态)。
箱线图的价值
箱线图包含的元素虽然有点复杂,但也正因为如此,它拥有许多独特的功能:
第一点,直观明了地识别数据批中的异常值。
箱线图用来捕获一组数据中的异常值,在数据整理的过程中,异常值带来的不良影响是巨大的,我们需要额外重视异常值这一数据,异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值,而箱线图会将这一部分的值额外展现出来,突出异常值的特异性。
第二点,利用箱线图判断数据批的偏态和尾重。
通过箱线图的形状和异常值的分布,我们可以大致的观测出这一组数据的偏态和尾重,然后通过对比标准正态分布,来分析数据形状的出现原因。
第三点,利用箱线图比较几批数据的形态。
将几批数据放在同一个数轴上,可以直观的看出几批数据之间中位数、尾长、异常值、分布区间等的不同,用于质量管理、人事测评、探索性数据分析等统计分析活动中,有助于分析过程的简便快捷,其作用显而易见。
凭借着这些“独门绝技”,箱线图在使用场景上也很不一般,最常见的是用于质量管理、人事测评、探索性数据分析等统计分析活动。